The best Pokémon party
- 8. December 2021 (modified 11. December 2021)
- #optimization, #datascience
In this article we’ll use optimization to create a really good Pokémon party. If you prefer watching a presentation rather than reading, this article has an accompanying YouTube recording.
I played Pokémon games when I was younger, and I’ve played the first three generations of games several times over the years. As a result, I am genuinely curious what the best Pokémon party is.
This article will introduce some simple and powerful techniques for mathematical optimization. This will be needed since the number of possible Pokémon parties (in the second generation) is
This is a huge number, so complete enumeration of the search space is out of the question.
First we will deal with Generation I while also spending some time setting up the problem. Then we’ll run the same calculations for generations II and III, making some additional comments. Let’s get to work!
Generation I: Pokémon Red and Blue
The first generation of Pokémon games featured \(151\) Pokémon, including Mew and Mewtwo. Each Pokémon has the following \(6\) base stats:
- hp
- attack
- defense
- special attack
- special defense
- speed
Each Pokémon has one or two types, such as Poison, Rock or Fire. In Generation I, there are \(15\) distinct types. Although there are \(\binom{15}{1} + \binom{15}{2} = 120\) possible ways a Pokémon can have one or two types, only \(34\) combinations of types are actually found in the Generation I games.
The Pokémon data can be organized in a table like this:
| number | name | hp | att | def | sp_att | sp_def | speed | type1 | type2 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Bulbasaur | 45 | 49 | 49 | 65 | 65 | 45 | Grass | Poison |
| 2 | Ivysaur | 60 | 62 | 63 | 80 | 80 | 60 | Grass | Poison |
| 3 | Venusaur | 80 | 82 | 83 | 100 | 100 | 80 | Grass | Poison |
| … | … | … | … | … | … | … | … | … | … |
| 149 | Dragonite | 91 | 134 | 95 | 100 | 100 | 80 | Dragon | Flying |
| 150 | Mewtwo | 106 | 110 | 90 | 154 | 154 | 130 | Psychic | None |
| 151 | Mew | 100 | 100 | 100 | 100 | 100 | 100 | Psychic | None |
A player may battle with \(6\) Pokémon, and these Pokémon comprise a party.
What is the best party? Let’s establish a way to evaluate a party, i.e. a function that assigns a value to a party indicating how good it is.
Highest stats
A first idea might be to use the stats for each Pokémon.
The \(6\) Pokémon with the highest stats are:
['Mewtwo', 'Moltres', 'Zapdos', 'Articuno', 'Dragonite', 'Mew']

This is certainly not a bad party, but I believe we can do better if we use type information.
Type advantage
There is a problem with using total stats as the only measure of how good a party is. The approach does not take into account the Pokémon types, such as Fire, Water, Fighting, Normal, Ghost, etc.
We’ll make some assumptions about what we mean by a “good” party. You could argue against these choices, but I believe they are sensible and help us establish a good model:
- We assume that our party of \(6\) is equally likely to meet any Pokémon in battle. We want to be well prepared no matter which opponent we meet.
- We ignore the types of the moves themselves (e.g. Earthquake is a Ground-type move). Instead we assume that a Pokémon of a certain type only has moves of the same type. For instance, we assume that a Fire-type Pokémon will only have Fire-type moves. A Bug and Grass Pokémon is assumed to have both Bug and Grass moves in its arsenal.
The first assumption is not valid if we’re looking for the best party to play through the game with, since some Pokémon appear way more frequently than others. The second assumption is not true in general, but it’s a decent approximation. It would be possible to include move-types in this analysis, but it requires more data and is more complex.
A type chart shows which moves are super effective (\(2\times\) damage), normal (\(1\times\) damage), not-very-effective (\(0.5 \times\) damage) and has no effect (\(0 \times\) damage) against other types. If the Pokémon party above based on total stats meets a Fire-type such as Charmeleon, it will not have any type advantage.
The attack advantage of Pokémon \(i\) when it meets Pokémon \(j\) in battle is a number in the set the \(\{1/8, 1/4, 1/2, 1, 2, 4\}\). It can be computed like this:
def attack_advantage(pokemon_i, pokemon_j):
"""Multiplier for damage when Pokémon i attacks Pokémon j."""
best_attack_factor = 1/8
for attack_type in pokemon_i.types:
attack_factor = 1
for defense_type in pokemon_j.types:
attack_factor *= type_chart[attack_type][defense_type]
best_attack_factor = max(best_attack_factor, attack_factor)
return best_attack_factor
Here is a graphical example showing the attack advantage of Golem against Bulbasaur:
 Turning the tables around, here is the attack advantage of Bulbasaur against Golem:
Turning the tables around, here is the attack advantage of Bulbasaur against Golem:

Notice how no-effect moves are given a factor of \(1/8\) instead of \(0\). A factor of \(1/8\) is more convenient for the calculations, and it’s not unreasonable to hope that for instance a Normal-type Pokémon will have some non-Normal move in its move set—making a factor of \(0\) too pessimistic.
Consider again the Pokémon party obtained by looking at total stats:

The first table below shows the party’s attack advantage against all other \(151\) Pokémon. The second table reverses the situation–it shows the other Pokémon’s attack advantage against the party. No single Pokémon in our party is bad, but they are too similar to play a distinct role as a party member.
In the top table above, the numbers on the right side of each row show the average attack advantage of each individual Pokémon. This average is computed using a geometric average along each row, and will be explained in further detail a bit later in the article. The number in the square brackets show the Shapley value—a measure of how much each Pokémon contributes to the party’s average attack advantage. The sum of the Shapley values \(0.23 + 0.21 + \cdots + 0.23\) equals the average attack advantage of the party as a whole, here equal to \(1.68\). You can find my implementation of the Shapley value here.
In the bottom table above, a green cell means the column Pokémon \(j\) has a great attack advantage against Pokémon \(i\) in the party. The numbers on the right side of each row show the average defense advantage of each individual Pokémon, defined as \(\text{def_adv}(i, j) = 1/\text{att_adv}(j, i)\). Higher numbers are better for the party, and again the numbers in the square brackets are the Shapley values.
The edge (overall advantage) of a Pokémon party
We can summarize the tables above into a single table, by defining the edge (overall advantage) of Pokémon \(i\) when it meets Pokémon \(j\) as:
If \(\text{edge}(i, j) > 1\), then Pokémon \(i\) has an overall advantage against Pokémon \(j\). Conversely, if \(\text{edge}(i, j) < 1\), then Pokémon \(j\) has an overall advantage against Pokémon \(i\). If \(\text{edge}(i, j) = 1\), then neither Pokémon has an advantage. This happens for instance when two Normal Pokémon meet and neither has any attack advantage, or if they are both super-effective against each other (for instance if two Ghost Pokémon meet—Ghost is super effective against Ghost).
The edge when Golem meets Bulbasaurs indicates that Bulbasaur is likely to win:

Here’s a table showing the edge of our party above against all \(151\) Pokémon:
The bottom row above, labeled “BEST EDGE” is defined as the maximum over each row:
This row represents the best edge the party can achieve against an opponent Pokémon, if we switch to the Pokémon in the party with the greatest edge. The average edge, seen in the title of the figure, is defined as \(\operatorname{geom\_avg}_j \text{BEST EDGE}_j\), and this number represents how good the party is overall.
Comment on geometric average. Above we use the geometric average instead of the arithmetic average. To see why this makes sense, consider two \(\text{BEST EDGE}\) arrays over \(3\) opponent Pokémon:
Which is better? I would prefer \(b\) over \(a\), but the arithmetic average is identical. The geometric average \(\operatorname{geom\_avg}_j \left( y_1, y_2, \ldots, y_n \right) = \left( y_1 y_2 \cdots y_n \right)^{1/n}\) prefers \(b\) over \(a\). We get \(\operatorname{geom\_avg} \left(1, 1, 8 \right) = 8^{1/3} = 2\) and \(\operatorname{geom\_avg} \left( 2, 4, 4\right) = 32^{1/3} = 2 \times 2^{1/3}\).
We optimize a bi-objective function \((\text{average_edge}, \text{average_stats})\) by prioritizing the first component and using the second component to resolve ties. In other words: if the edge is equal, we prefer a party with higher average stats.
A greedy approach
Since there are \(\binom{151}{6} = 14\,888\,600\,755\) possible parties, complete enumeration is not feasible. Let’s start with a greedy approach:
Greedy algorithm. We consider all \(151\) Pokémon and find the one that gives the best average edge alone. We add this Pokémon to the party. Then we check the remaining \(150\) Pokémon. Again we add the one that gives the best average edge in combination with the first choice. We continue this process until we have a party of \(6\).
In this process we must consider \(151 + 150 + 149 + 148 + 147 + 146 = 891\) Pokémon, which is feasible.
The solution is:
['Gyarados', 'Rhydon', 'Exeggutor', 'Gengar', 'Omastar', 'Venomoth']

The attack and defense table of this party is shown below:
Gyarados is chosen first. It has a nice balance between attack advantage and defense advantage. Next Rhydon is chosen, and we can see that it complements Gyarados nicely. The process continues until a full party is chosen.
Here is the greedy party’s edge against all other Pokémon:
This is a good party! The average edge is \(4.87\), compared to \(1.95\) for the party chosen based on stats alone. No matter what opponent this party meets, it never has a disadvantage. In most cases it has a big edge.
Pareto-Pokémon
Recall that there are \(\binom{151}{6} = 14\,888\,600\,755\) possible parties. This is a large number, but we can reduce the search space drastically if we make a simple observation.
Consider a row Pokémon \(i\) and another row Pokémon \(k\). If \(\text{edge}(i, j) \geq \text{edge}(k, j)\) for all \(j\) and the total stats of Pokémon \(i\) is greater than or equal to Pokémon \(k\), then there is no reason to ever consider Pokémon \(k\). In many such cases \(\text{edge}(i, j) > \text{edge}(k, j)\) for at least one \(j\), but even if no such \(j\) exists there is still no reason to keep Pokémon \(k\).
The Pokémon \(k\) was Pareto-dominated by Pokémon \(i\). We call the non-dominated choices Pareto-Pokémon. Want to learn more about Pareto sets? Read my article “Pareto non-dominated front as a consumer strategy” and check out my Python package paretoset.
Out of \(151\) Pokémon, only \(30\) are Pareto-Pokémon. These Pokémon are not dominated by any other:



The exhaustive search is now reduced to \(\binom{30}{6} = 593\,775\) parties. This represents a reduction of the search space to \(0.004 \%\) of its original size. Running a complete enumeration shows that the best party is:

Here is the edge table for the best party (sorted by Shapley value):
Notice that the average edge of this party is \(4.99\), compared with \(4.87\) for the greedy solution and \(1.95\) for the party based on total stats.
Mixed Integer Program
This section is a bit math-heavy and can be skipped without loss of continuity.
I’ll quickly sketch how we can formulate the optimization problem above as a Mixed Integer Program (MIP). The structure of the program is to maximize a \(\max\) function (the BEST EDGE), and the tricky part is to linearize this \(\max\) function.
Let \(x_i \in \{0 , 1\}\) denote whether Pokémon \(i\) is chosen for the party. The constraint \(\sum_i x_i = 6\) says that we have to choose \(6\) Pokémon. The optimization problem can be written as:
We will now formulate this as a MIP.
Let \(e_{ij} := \ln \text{edge}(i, j)\) be the edge of Pokémon when it battles Pokémon \(j\). Let \(y_j := \max_i e_{ij} x_i\). In other words, \(y_j\) gives the party’s best advantage over Pokémon \(j\). We want to maximize the sum over all \(y_j\), which is equivalent to maximizing the geometric mean.
The \(\max\) function must be linearized, so we introduce variables \(z_{ij} \in \{0 , 1\}\) and add the following constraints:
The number \(M\) is an upper bound on the range of the variables \(e_{ij}\). If \(z_{ij} = 1\) for a given \(j\), then \(e_{ij} x_i\) is the maximum variable. This requires some thought, but you can see that it’s correct.
The optimization problem formulated as a MIP is:
The tie breaker using total stats is included as a second term in the objective function, where \(\epsilon\) is a small number. This causes the MIP to prioritize the first term in the objective over the second. In practice complete enumeration of parties consisting of Pareto-Pokémon was faster than actually solving this MIP.
Solution approach
Here are three approaches to obtaining an optimal solution, in increasing order of efficiency:
- Check every one of the \(\binom{151}{6} = 14\,888\,600\,755\) possible parties. This would take around 5 days on my computer, and is not feasible at all.
- Remove Pareto-dominated Pokémon, then check every one of the \(\binom{30}{6} = 593\,775\) combinations. This would take 18 seconds.
- Remove Pareto-dominated Pokémon, then run branch-and-bound. My simple branch-and-bound implementation took 0.4 seconds.
If an approximate solution is good enough, then a greedy algorithm or simulated annealing will both do well. The figure below shows the structure of the branch-and-bound search. A total of \(373\) nodes were popped off the priority queue during the search—a great improvement compared to examining almost \(15\) billion combinations.

Generation II: Pokémon Gold and Silver
Let’s examine the next generation, which includes \(251\) Pokémon in total. The Steel type was also added. Apart from that, our approach will largely be the same.
Greedy approach
Let’s try a greedy approach first, but with a twist. Instead of stopping at \(6\) party members, we examine for how long we can add Pokémon until the average edge of the party does not increase any further. The result, in order of selected Pokémon, is shown below:


Here’s how the objective function increases as we add Pokémon. Notice the diminishing returns of adding more and more Pokémon.

Of course we have to stop after \(6\) Pokémon, since the \(16\) Pokémon suggested by the greedy algorithm are too many. Here is the edge table for the greedily chosen party of \(6\) (click to enlarge):
Best party by enumeration of the Pareto-Pokémon
Once again the search space is large. There are \(\binom{251}{6} = 327\,012\,476\,050\) possible parties. We’ll limit ourselves to Pareto-Pokémon to reduce the search. There are \(55\) Pareto-Pokémon, which means that we have to check \(\binom{55}{6} = 28\,989\,675\) possible parties. This takes some time, but is completely feasible with some patience.
The best party
The best possible party is: ['Celebi', 'Skarmory', 'Gengar', 'Steelix', 'Tyranitar', 'Magcargo']

The edge of this party (click on image to enlarge) is shown below:
 Notice that the best party is not equal to the greedily selected party, which achieved an average edge of \(5.86\).
Notice that the best party is not equal to the greedily selected party, which achieved an average edge of \(5.86\).
The best party that can be found in-game
The first Pokémon above is Celebi, which cannot actually be found in-game. Here is the best party where each Pokémon can be found in both the Gold and Silver games. We examine the best party for each possible size of a party from \(1\) to \(6\). It’s interesting to see that Pokémon such as Magneton appears, then disappears.






Here is the edge table. The average edge of this party, where all Pokémon can be found in-game, is \(5.57\). Not a large drop from the party above which had \(5.99\).
The worst party
In case you’re curious, the worst party that can be found in-game is:
['Girafarig', 'Abra', 'Weedle', 'Caterpie', 'Igglybuff', 'Nidoran-M']

Looking at the edge table, we can see that it’s indeed very bad. The selected Pokémon are individually bad, and they do not complement each other well as a team.
Generation III: Pokémon Ruby and Sapphire
Finally, let’s briefly look at the third generation, which has \(200\) Pokémon.
Greedy party
Here’s what the greedy algorithm proposes if we run it. Again we do not stop after obtaining a party of \(6\), but examine for how long we can add Pokémon until the average edge of the party does not increase any further.


Here’s the edge table for the first \(6\) Pokémon:
The best party
The greedily chosen part is not the best party.
The best party is:
['Sableye', 'Skarmory', 'Swampert', 'Aggron', 'Ludicolo', 'Breloom']

Here’s the edge table for this party. We see that the best party is only slightly better than the greedy party.
Best party found in-game
Here is the best party where each Pokémon can be found in both the Ruby and Sapphire games, for each possible size from \(1\) to \(6\).






Here’s the edge table for the party of \(6\):
Tradeoff between edge and average total stats
The party above has \((\text{average_edge}, \text{average_stats}) = (5.48, 450.17)\). If we want to trade some edge-advantage in favor of higher stats, that’s possible. Each dot in the figure below shows a party in the Pareto set in the \((\text{average_edge}, \text{average_stats})\)-space:
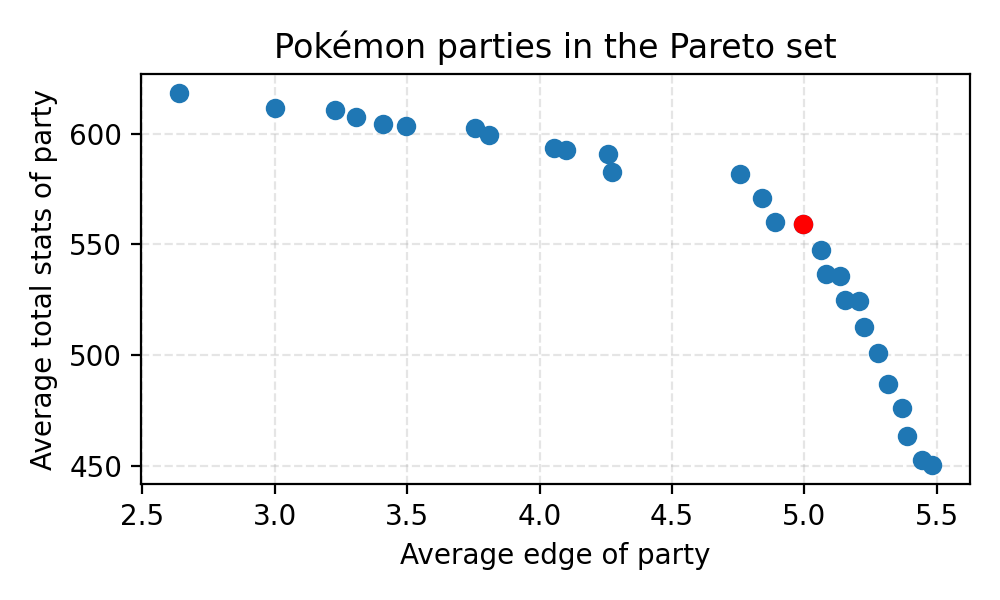
If we choose the red party above, we obtain a reasonable tradeoff:

Tradeoff between attack and defense advantage
It’s also possible to look for Pareto-parties in the space of:
This might be relevant if you wish to trade some attack advantage for defense advantage or vice versa. Interestingly, only \(10\) parties are non-dominated.

Notes
- The blogpost “Choosing the perfect Pokémon team with Python and PuLP” introduces a similar approach, but uses a concept of resistance. The idea is to choose Pokémon by total stats, subject to the constraint that each party member is resistant to at least one attack type. In a follow-up post the author considers five different objectives.
- Instead of maximizing the average maximum edge, we could maximize the average maximum attack advantage of the Pokémon party, or we could minimize the average minimum attack advantage against the Pokémon party. I chose to mainly work with the edge because it captures both elements of attack and defense against types, but other choices are possible. It’s also possible to add moves to the analysis.
- I could not find any good Python implementation of the Shapley value algorithm. As a result I ended up writing my own simple implementation, which you are welcome to look at and use.
- We solve a problem similar to the maximum coverage problem in this article. It’s well known that the greedy algorithm achieves an approximation factor of \((1 - 1/e) \approx 0.632\) on the maximum coverage problem. This is problem 2.18 in the book “Approximation Algorithms” by Vazirani.
Appendix: Pareto-Pokémon for each game
Out of all the Pokémon that can be obtained in both games and in each version, these plots display the Pareto-Pokémon.
Generation I



Best party by edge (attack and defense advantage)

Best party by attack advantage

Best party by defense advantage

Generation II






Best party by edge (attack and defense advantage)

Best party by attack advantage

Best party by defense advantage

Generation III






Best party by edge (attack and defense advantage)

Best party by attack advantage

Best party by defense advantage




















